- Peluang Suatu Kejadian
Jika A adalah suatu kejadian yang terjadi pada suatu percobaan dengan ruang sampel S,dimana setiap titik sampelnya mempunyai kemungkinan sama untuk muncul, maka peluang dari suatu kejadian A dirumuskan sebagai berikut: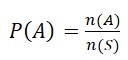
dengan P(A) = peluang kejadian A, n(A) = banyaknya anggota kejadian A, n(S) = banyaknya anggota ruang sampel.
Contoh:
Dua buah dadu dilempar satu kali secara bersama-sama. Tentukan peluang munculnya mata dadu berjumlah bilangan genap!
Jawab:
n(S) = 36
A = {(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3), (5,5), (6,2), (6,4), (6,6)}
n(A) = 18
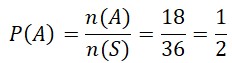
Jadi, peluang muncul mata dadu berjumlah bilangan genap adalah ![]()
- Peluang Komplemen
Jika A adalah kejadian dari himpunan S, maka kejadian bukan A juga merupakan himpunan bagian dari himpunan S. Kejadian bukan A dinotasikan dengan A’ atau Ac (dibaca komplemen). Jika Ac adalah komplemen kejadian A, maka peluang Ac ditentukan dengan aturan:
![]()
Contoh:
Sebanyak 24 kartu diberi nomor 1 sampai 24. Tentukan peluang terambilnya kartu bukan faktor dari 20!
Jawab:
n(S) = 24
A = kartu bernomor yang merupakan faktor dari 20 = {1, 2, 4, 5, 10, 20}, n(A) = 6
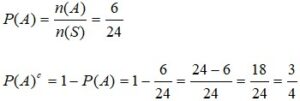
- Peluang Kejadian Majemuk
Kejadian saling lepas dan tidak saling lepas
Dua kejadia A dan B dikatakan saling lepas jika kejadian A dan B tidak dapat terjadi secara bersama-sama. Jika A dan B saling lepas maka
![]()
Jika kejadian A dan B saling lepas, maka peluang kejadian A atau B dirumuskan sebagai berikut.
![]()
Contoh:
Dua dadu dilambungkan bersamaan sekaligus sekali. Tentukan peluang muncul mata dadu berjumlah 3 atau 10.
Jawab:
n(S) = 36
A = kejadian muncul mata dadu berjumlah 3 = {(1,2), (2,1)} n(A)=2
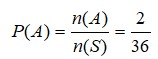
B = Kejadian muncul mata dadu berjumlah 10 = {(4,6),(5,5),(6,4)} n(B)=3
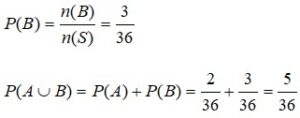
Dua kejadian A dan B dikatakan tidak saling lepas jika kejadian A dan B dapat terjadi secara bersama sama. Jika A dan B tidak saling lepas, maka . Jika kejadian A dan B tidak saling lepas, maka peluang kejadian A atau B dirumuskan sebagai berikut.
![]()
Contoh:
Pada percobaan melempar sebuah dadudan satu keping uang logam, tentukan peluang munculnya mata dadu > 3 atau gambar!
Jawab:
n(S) = 12
A = kejadian muncul dadu > 3 ={(A,4), (A,5), (A,6), (G,4), (G,5), (G,6)}, n(A) = 6
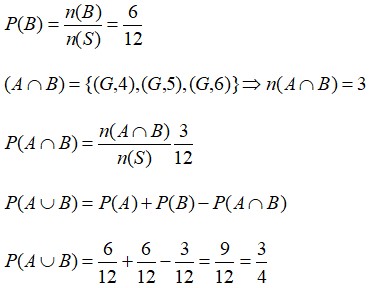
Kejadian saling bebas dan bersyarat
Dua kejadian A dan B yang terjadi secara berurutan dikatakan saling bebas apabila kejadian A tidak mempengaruhi peluang terjadinya kejadian B. Apabila A dan B adalah dua kejadian saling bebas, maka peluang terjadinya kejadian A dan B dirumuskan sebagai berikut.
P(A∩B) = P(A) x P(B)
Contoh:
Dua buah dadu dilempar satu kali secara bersama-sama. Tentukan peluang munculnya mata dadu pertama bilangan prima dan mata dadu kedua bilangan genap!
Jawab:
n (S) = 36
A = muncul mata dadu pertama bilangan prima
A = {(2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (5,1), (5,2), (5,3), (5,4), (5,6)}, n(A) = 18
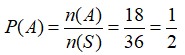
B = muncul kedua bilangan genap
B = {(2,2), (2,4), (2,6), (4,2), (4,4), (4,6), (6,2), (6,4), (6,6)}, n (B) = 9
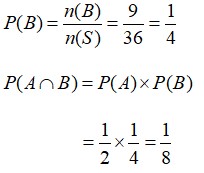
4. Frekuensi Harapan
Frekensi harapan suatu kejadian adalah hasil kali banyak percobaan (n) dengan peluang kejadian tersebut. Dengan demikian frekuensi harapan kejadian A atau Fh(A), dari suatu percobaan yang dilakukan sebanyak n kali dengan P(A) dirumuskan sebagai berikut:
Fh(A) = n x P(A)
Fh(A) = frekuensi harapan kejadian A
n = benyaknya percobaan
P (A) = peluang kejadian A
– Sumber: Prediksi UN SMK, Dicetak oleh : Putra Nugraha –
